Logaritma merupakan fungsi invers dari eksponen.
 Dengan a = bilangan pokok ,
Dengan a = bilangan pokok ,  yang merupakan invers (cerminan dari f(x) terhadap garis y = b) dari fungsi eksponen
yang merupakan invers (cerminan dari f(x) terhadap garis y = b) dari fungsi eksponen  , sehingga
, sehingga  mempunyai invers
mempunyai invers  .
.

 .
.





 yang merupakan invers (cerminan dari f(x) terhadap garis y = b) dari fungsi eksponen
yang merupakan invers (cerminan dari f(x) terhadap garis y = b) dari fungsi eksponen  , sehingga
, sehingga  mempunyai invers
mempunyai invers  .
.
I. Sifat-sifat Logaritma
a. Sifat Perkalian Logaritma
Perkalian logaritma samadengan penjumlahan logaritma dengan basis tetap.

b.Sifat Pembagian Logaritma
Jika hasil logaritma merupakan pembagian,hasilnya dapat diuraikan menjadi operasi pengurangan bilangan logaritma dengan basis tetap.
 .
.
c. Sifat Perpangkatan Logaritma
Hasil operasi berupa bilangan logaritma berpangkat, dapat diuraikan sbb:

d. Sifat Penarikan Akar
Jika ada hasil operasi logaritma yang berbentuk akar, ubahlah terlebih
dahulu menjadi bentuk pangkat untuk mempermudah penyelesaianya.

Beberapa Sifat Logaritma yang lain:

II. Persamaan Logaritma

III. Pertidaksamaan Logaritma




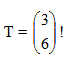




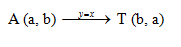














 adalah
adalah 
